Exercise 1.14 -- 1.15

Exercise 1.14

Draw the tree illustrating the process generated by the count-change procedure of Section 1.2.2 in making change for 11 cents. What are the orders of growth of the space and the number of steps used by this process as the amount to be changed increases.

Solution

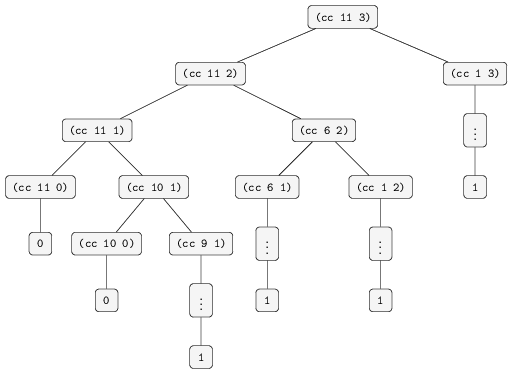
Tikz code for image on GitHub.

Exercise 1.15

The sine of an angle (in radians) can be computed by making use of the approximation $\sin x\approx x$ if $x$ is sufficiently small, and the trigonometric identity

to reduce the size of the argument of $\sin$.(For the purposes of this exercise an angle is considered “sufficiently small” if its magnitude is not greater than 0.1 radians.) These ideas are incorporated in the following procedures:

(define (cube x) (* x x x))
(define (p x) (- (3 x) (* 4 (cube x))))
(define (sine angle)
    (if (not (> (abs angle) 0.1))
        angle
        (p (sine (/ angle 3.0)))))

1. How many times is the procedure p applied when (sine 12.15) is evaluated?
2. What is the order of growth in space and number of steps (as a function of $a$) used by the process generated by this sine procedure when (sine a) is evaluated?

Solution

1. The procedure p is applied the same numbers of times as the angle needs to be divided by 3 before the result is less that 0.1 radians. So p is applied 5 times in the evaluation of (sine 12.15).
2. From the first part of the exercise we see that (sine n) is $\Theta(\log n)$ in space and since the procedure is a linear recursion the procedure is also $\Theta(\log n)$ in space.