2.2a The Picture Language: painters

To implement the painters in the picture language we use Script-Fu, which is a Scheme scripting console available in Gimp. The implementation is by no means complete, the two main issues being:

the segements->painter procedure is not implemented; and
the frames that painters can accept as arguments has been restricted.

Restricted frames

To make the implementation of painters eaiser, while still being able to be manipulated by higher-order functions such as square-limit, the frames that painters can accept have been restricted. Frames accepted by painters must

have edges orthogonal to each other; and
be square with the canvas.

That is, for a frame (make-frame origin edge1 edge2), the dot product of edge1 and edge2 must be zero and edge1, edge2 are scalar multiples of one of the basis vectors, $\mathbf i,\mathbf j$. Generally the scalar multiple we will be between -1 and 1.

To test for these conditions two additional procedures for vectors have been defined: len-vec, which takes a vector, $\mathbf v=(x, y)$ as argument and returns the length of the vector as given by

$\lVert \mathbf v\rVert = \sqrt{x^2 + y^2}$

(define (len-vect v)
  (sqrt (+ (square (xcor-vect v))
           (square (ycor-vect v)))))

dot-product takes two vectors as arguments, $\mathbf v=(x_1,y_1), \mathbf u=(x_2,y_2)$ and returns the dot product of the two

$\mathbf v\cdot \mathbf u = x_1x_2 + y_1y_2$

(define (dot-product u v)
  (+ (* (xcor-vect u) (xcor-vect v))
     (* (ycor-vect u) (ycor-vect v))))

The restrictions we place on the frame, means that we must have

(and (= 0 (dot-product edge1 edge2))
     (= (len-vect edge1)
        (+ (abs (xcor-vect edge1))
           (abs (ycor-vect edge1)))))

Note that to show that edge1 is a multiple of a basis vector we show that the length of the edge1 is the same as measured by the euclidean and manhattan distances.

Frames and transformations

Unfortunately Gimp/Script-Fu does not have structures analogous to frames that can be used to manipulate images, but instead, has provided procedures such as gimp-image-scale, gimp-image-flip and gimp-image-rotate. So to define painters we need to do the reverse of what we have been doing in SICP: instead of expressing image transformations through frame manipulations, we need to determine the transformations that have been applied to produce a given frame.

For example, painters need to recognize that the following frame means that no transformations to the image need to be performed;

(make-frame
  (make-vect 0 0)
  (make-vect 1 0)
  (make-vect 0 1))

Untransformed frame

that the following frame means that the image needs to be scale so as to fit the bottom left-hand quarter of the canvas;

(make-frame
  (make-vect 0 0)
  (make-vect 0.5 0)
  (make-vect 0 0.5))

Scaled frame

and that the following frame means that the image needs to be rotated and flipped.

(make-frame
  (make-vect 0 0)
  (make-vect 0 1)
  (make-vect 1 0))

Rotated and flipped frame

It turns out the all the effects of the procedures demonstrated in the picture language, from beside and below to square-limit, can be achieved using a combination of scaling, horizontal flips and 90 degree counter-clockwise rotations. Furthermore, each of these transformations modifies the frame in a unique and identifiable way.

Transformation matrices

Let the edges of a frame be the rows of a matrix, so that

$E = \begin{pmatrix} \mathbf e_1\\ \mathbf e_2 \end{pmatrix} = \begin{pmatrix} x_1 & y_1\\ x_2 & y_2 \end{pmatrix}$

Then the act of flipping and rotating frames can be represented as applying a transformation to the edges matrix

$t(E) = ET$

for some transformation matrix $T$. Furthermore, for a transformation, we can find the inverse transformation, such that

$t^{-1}(t(E)) = ETT^{-1} = E$

where $T^{-1}$ is the matrix inverse of $T$.

Rotation

To rotate the edges $E$ by $\theta$ radians clockwise, the following transformation matrix is used:

$T_{\mathrm{rot}(\theta)} = \begin{pmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}$

In particular, to rotate the frame 90 degrees counter-clockwise

$T_{\mathrm{rot}(90)} = \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}$

and the inverse transform

$T^{-1}_{\mathrm{rot}(90)} = \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}^{-1} = \begin{pmatrix} 0 & -1\\ 1 & 0 \end{pmatrix}$

Thus, when a frame with edges, $E_R$, that produces an image rotated $n$ quarter turns counter-clockwise, is supplied to a painter, without knowing $n$ beforehand we can calculate the correct number of rotations by counting the number of applications of the inverse rotation transform before the we result in the identity matrix, that is

$E_RT_{\mathrm{rot}(90)}^{-n} = I$

Horizontal flip

The transformation matrix used to flip the edges of a frame horizontally is

$T_{\mathrm{hori}} = \begin{pmatrix} -1 & 0\\ 0 & 1 \end{pmatrix}$

and the inverse transformation matrix is the same as the transform, that is, two horizontal flips will result in an unchanged image.

Next we determine when a frame has been flipped. The figure below shows a frame that has been flipped horizontally.

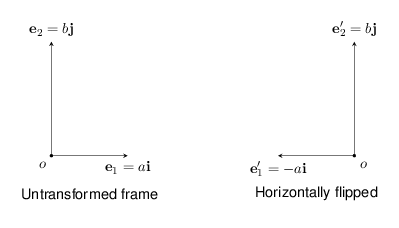
Horizontally flipped frame

We note that by flipping the frame, the angle from $\mathbf e_1$ and $\mathbf e_2$, measured in the counter-clockwise direction, has changed. This has the effect of changing the sign/direction of the cross product of the two edges. That is,

$\begin{align} \hat{\mathbf e}_1\times\hat{\mathbf e}_2 &= c\mathbf k\\ \hat{\mathbf e}_1'\times\hat{\mathbf e}_2' &= -c\mathbf k \end{align}$ for some $c>0$.

So to determine whether a frame has been flipped we only need to look at the sign of the cross product of the edges, and since our edges are multiples of basis vectors this is the same the sign of the determinant of 2x2 matrix with the edges as rows,

$\mathrm{det}\left(\begin{bmatrix} \mathbf e_1\\ \mathbf e_2 \end{bmatrix}\right)$

(define (det u v)
  (- (* (xcor-vect u) (ycor-vect v))
     (* (ycor-vect u) (xcor-vect v))))

:testSite

work in progress