Exercise 2.7 -- 2.16
Exercise 2.7
Alyssa’s program is incomplete because she has not specified the implementation of the interval abstraction. Here is a definition of the interval constructor:
(define (make-interval a b) (cons a b)Define selectors upper-bound and lower-bound to complete the
implementation.
Solution
(define (upper-bound x)
(max (car x) (cdr x)))
(define (lower-bound x)
(min (car x) (cdr x)))Exercise 2.8
Using reasoning analogous to Alyssa’s, decribe how the difference of
two intervals may be computed. Define a corresponding subtraction
procedure, called sub-interval.
Solution
Similar to div-interval, the difference of two intervals $x$ and $y$
(that is, $x-y$) has an upper bound when the lower bound of $y$ is
subtracted from the upper bound of $x$, and the lower bound is
achieved when the upper bound of $y$ is substracted from the lower
bound of $x$.
(define (sub-interval x y)
(make-interval (- (lower-bound x) (upper-bound y))
(- (upper-bound x) (lower-bound y))))Exercise 2.9
The width of an interval is half of the difference between its upper and lower bounds. The width is a measure of the uncertainty of the numbers specified by the interval. For some arithmetic operations the width of the results of combining two intervals is a function only of the widths of the argument intervals, whereas for others the width is not a function of the widths of the argument intervals. Show that the width of the sum (or difference) of two intervals is a function only of the widths of the intervals being added (or subtracted). Give examples to show that this is not true for multiplication or divison.
Solution
For intervals $a=[a_l,a_u]$, $b=[b_l,b_u]$, let $c=a+b$ where
then the width of $c$ can be expressed as
that is the width of $c$ is a function completely specified by the width of $a$ and $b$, in particular it is the sum of the width of $a$ and $b$.
To show that this is not the case when multiplying two intervals, consider $a=[0,1]$ and $b=[1,2]$ then
(define a (make-interval 0 1))
(define b (make-interval 1 2))
(mul-interval a b)
; (0 . 2)If we shift the interval $b$ up by one unit so that $b=[2,3]$ and the width of $b$ remains the same
(define b (make-interval 2 3))
(mul-interval a b)
; (0 . 3)Exercise 2.10
Ben Bitdiddle, an expert systems programmer, looks over Alyssa’s shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Modify Alyssa’s code to check for this condition and to signal an error if it occurs.
Solution
(define (div-interval x y)
(if (> (* (lower-bound y) (upper-bound y)) 0)
(mul-interval x
(make-interval (/ 1.0 (upper-bound y))
(/ 1.0 (lower-bound y))))
(error "dividing by an interval containing zero" y)))Exercise 2.11
In passing, Ben also cryptically comments: “By testing the signs of
the end points of the intervals, it is also possible to break
mul-interval into nine cases, only one of which requires more than
two multiplications”. Rewrite this procedure using Ben’s suggestion.
Solution
For a single interval there are three different configurations for the signs of the endpoints:
The different combinations for a pair of intervals gives us the 9 cases. This can be represented as the following tree and procedure
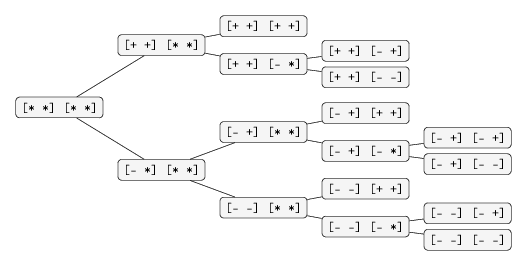
Tikz code for figure on GitHub.
(define (mul-interval1 x y)
(if (> (lower-bound x) 0)
(if (> (lower-bound y) 0)
(make-interval (* (lower-bound x) (lower-bound y))
(* (upper-bound x) (upper-bound y)))
(if (> (upper-bound y) 0)
(make-interval (* (upper-bound x) (lower-bound y))
(* (upper-bound x) (upper-bound y)))
(make-interval (* (upper-bound x) (lower-bound y))
(* (lower-bound x) (upper-bound y)))))
(if (> (upper-bound x) 0)
(if (> (lower-bound y) 0)
(make-interval (* (lower-bound x) (upper-bound y))
(* (upper-bound x) (upper-bound y)))
(if (> (upper-bound y) 0)
(make-interval (min (* (upper-bound x) (lower-bound y))
(* (lower-bound x) (upper-bound y)))
(max (* (lower-bound x) (lower-bound y))
(* (upper-bound x) (upper-bound y))))
(make-interval (* (upper-bound x) (lower-bound y))
(* (lower-bound x) (lower-bound y)))))
(if (> (lower-bound y) 0)
(make-interval (* (lower-bound x) (upper-bound y))
(* (upper-bound x) (lower-bound y)))
(if (> (upper-bound y) 0)
(make-interval (* (upper-bound x) (upper-bound y))
(* (upper-bound x) (lower-bound y)))
(make-interval (* (lower-bound x) (lower-bound y))
(* (upper-bound x) (upper-bound y))))))))Exercise 2.12
After debugging her program, Alyssa shows it to a potential user, who complains that her program solves the wrong problem. He wants a program that can deal with numbers represented as a center value and an additive tolerance; for example, he wants to work with intervals such as 3.5 ± 0.15 rather that [3.35,3.65]. Alyssa returns to her desk and fixes this problem by supplying an alternate constructor and alternative selectors:
(define (make-center-width c w)
(make-interval (- c w) (+ c w)))
(define (center i)
(/ (+ (lower-bound i) (upper-bound i)) 2))
(define (width i)
(/ (- (upper-bound i) (lower-bound i)) 2))Unfortunately, most of Alyssa’s users are eningeers. Real engineering situations usually involve measurements with only a small uncertainty, measured as the ratio of the width of the interval to the midpoint of the interval. Engineers usually specify percentage tolerances on the parameter devices, as in the resistor specifications given earlier.
Define a constructor make-center-percent that takes a center and a
percentage tolerance and produces the desired interval. You must also
define a selector percent that produces the percent tolerance for a
given interval. The center selector is the same as the one shown
above.
Solution
(define (make-center-percent c p)
(make-center-width c (* c p)))
(define (percent i)
(/ (width i) (center i)))Exercise 2.13
Show that under the assumption of small percentage tolerances there is a simple formula for the approximate percentage tolerance of the product of two intervals in terms of the tolerances of the fators. You may simplify the problem by assuming that all numbers are positive.
Solution
Let intervals be denoted by the pair $i=(i_c,i_p)$ where $i_c$ is the centre point of the interval and $i_p$ is the percentage tolerance of the interval. Given two intervals $a$ and $b$, if both intervals are positive, we saw in Exercise 2.11, the interval resulting from the product of $a$ and $b$
where $a_l$, $a_u$ are the lower and upper bounds of $a$.
So the percentage tolerance of the product interval is
If we assume that $a_p$ and $b_p$ are small then $a_pb_p$ may be ignored to give an approximate percentage tolerance of $a_p+b_p$.
Exercise 2.14
After considerable work, Alyssa P. Hacker delivers her finished system. Several years later, after she has forgotton all about it, she gets a frenzied call from an irate user, Lem E. Tweakit. It seems that Lem has noticed that the formula for parallel resistors can be written in two algebraiclly equivalent ways:
and
He has written the following two programs, each of which computes the parallel-resistors formula differently:
(define (par1 r1 r2)
(div-interval (mul-interval r1 r2)
(add-interval r1 r2)))
(define (par2 r1 r2)
(let ((one (make-interval 1 1)))
(div-interval one
(add-interval (div-interval one r1)
(div-interval one r2)))))Lem complains that Alyssa’s program gives different answers for the two ways of computing. This is a serious complaint.
Demonstrate that Lem is right. Investigate the behaviour of the system on a variety of arithmetic expressions. Make some intervals $A$ and $B$, and use them in computing the expressions $A/A$ and $A/B$. You will get the most insight by using intervals whose width is a small percentage of the center value. Examine the results of the computation in center-percent form.
Solution
Demonstrating Lem’s problem
(define (interval-to-center-percent i)
(cons (center i) (percent i)))
(define a (make-center-percent 1 0.01))
(define b (make-center-percent 2 0.02))
(interval-to-center-percent (par1 a b))
; (.6673186996387885 . 4.6637353852303345e-2)
(interval-to-center-percent (par2 a b))
; (.666651847735482 . 1.3334000200060044e-2)The centres are similar but tolerances are quite different.
If we look at the behaviour of the arithmetic operations on intervals that we have defined, we see that the resutling percentage tolerance when adding and subtracting intervals is an average of the two intervals weighted by their centers. When multiplying or dividing intervals, the resulting percentage tolerance is (approximately) the sum of the tolerances of two intervals.
For example:
(interval-to-center-percent (add-interval a a))
; (2. . 1.0000000000000009e-2)
(interval-to-center-percent (div-interval a a))
; (1.0002000200020003 . 1.9998000199980076e-2)
(interval-to-center-percent (add-interval a b))
; (3. . 1.6666666666666607e-2)
(interval-to-center-percent (div-interval a b))
; (.5003001200480192 . 2.9994001199760017e-2)Exercise 2.15
Eva Lu Ator, another user, has also noticed the different intervals
computed by different but algebraically equivalent expressions. She
says that a formula to compute with intervals using Alyssa’s system
will produce tighter error bounds if it can be written in such a form
that no variable that represents an uncertain number is repeated. Thus,
she says, par2 is a “better” program for parallel resistances than
par1. Is she right? Why?
Solution
TODO
Exercise 2.16
Explain, in general, why equivalent algebraic expressions may lead to different answers. Can you divise an interval-arithmetic package that does no have this shortcoming, or is this task impossible? (Warning: this problem is very difficult.)
Solution
TODO