1.2 Procedures and the Processes They Generate

In this chapter we take a step back from the procedure and say something about the overall, or global, behaviour of the process that is specified by the procedure. Global behaviours that we look at in this section are the common “shapes” generated by procedures and the rates of growth in time and space of procedures.

Linear Recursion and Iteration

Consider the factorial function:

$n! = n(n-1)(n-2)\ldots 3\cdot 2\cdot 1$

Two possible ways of calculating the function with illustrations of how the procedures evolved:

; first method
(define (factorial n)
    (if (= n 1)
        1
        (* n (factorial (- n 1)))))

(factorial 6)
(* 6 (factorial 5))
(* 6 (* 5 (factorial 4)))
(* 6 (* 5 (* 4 (factorial 3))))
(* 6 (* 5 (* 4 (* 3 (factorial 2)))))
(* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1))))))
(* 6 (* 5 (* 4 (* 3 (* 2 1)))))
(* 6 (* 5 (* 4 (* 3 2))))
(* 6 (* 5 (* 4 6)))
(* 6 (* 5 24))
(* 6 120)
720

; second method
(define (factorial n)
    (fact-iter 1 1 n))
(define (fact-iter product counter max-count)
    (if (> counter max-count)
        product
        (fact-iter (* counter product)
                   (+ counter 1)
                   max-count)))

(factorial 6)
(fact-iter 1 1 6)
(fact-iter 1 2 6)
(fact-iter 2 3 6)
(fact-iter 6 4 6)
(fact-iter 24 5 6)
(fact-iter 120 6 6)
(fact-iter 720 7 6)
720

Consider the first process: the substitution model reveals a wedge shape as the expression expands and contracts. The expansion occurs as the process builds up a chain of deferred operations, contraction occurs as the operations are performed. This type of process, characterised by a chain of deferred operations, is called a recursive process. Carrying out this process requires that the interpreter keep track of the operations to be performed later on. In this case, the computation of factorial creates a chain of deferred operations of length proportional to the input, so we called this a linear recursive process.

The second process revels a rectangular shape: at each step, all we need to keep track of are the current values of the variables in fact-iter. This type of process is called an iterative process. An iterative process is one whose state can be summarised by a fixed number of state variables, together with rules which describe how the state variables should be updated as the process moves from state to state and conditions which specify how the process will terminate. Again, the number of steps in the factorial procedure grows linearly with the input, so we call it a linear iterative process.

Note that in talking about iteration and recursion, there is a difference between a recursive process and a recursive procedure. When a procedure is descibed as recursive, we are referring to the syntactic fact that the procedure refers to itself in its definition. When a process is described as recursive, we are refering to the way the process evolves through deferred operations. So, for example, fact-iter is a recursive procedure but an iterative process.

Tree Recursion

Tree recursion is another common pattern in computation. A typical example of this pattern is produced by the following procedure for generating the Fibonacci sequence:

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

To compute (fib 5), we compute (fib 4) and (fib 3). To compute (fib 4), we compute (fib 3) and (fib 2). That is the process branches into two computations at each level (except at the bottom) reflecting the fact that the fib procedures calls itself twice each time it is invoked.

Fibonacci tree recursion

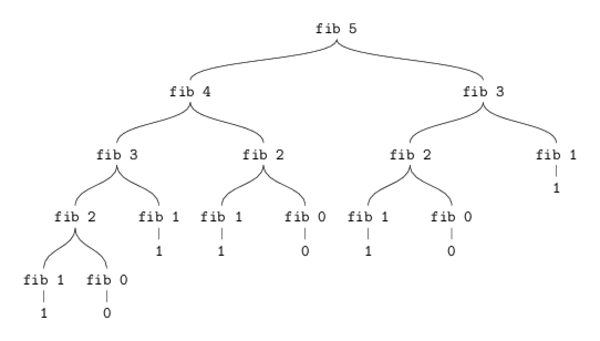
Tikz code for image on Github.

The process uses a number of steps that grows exponentially with the input. While the space required grows only linearly with the input as we need keep track only of which nodes are above us in the tree at any point in the computation. In general the number of steps required by a tree-recursive process wil be proportional to the number of nodes in the tree, while the space required will be proportional to the maximum depth of the tree.

Note: It was not clear to me why a tree recursive process would have space complexity proportional to the maximum depth, it seemed to me that space should be proportional to the number of leaves in the tree. I turns out that we should think of the interpreter evaluating a tree recursive process by travelling down only one branch at a time. For example,

(fib 5)
(+ (fib 4) (fib 3))
(+ (+ (fib 3) (fib 2)) (fib 3))
(+ (+ (+ (fib 2) (fib 1)) (fib 2)) (fib 3))
(+ (+ (+ (+ (fib 1) (fib 0)) (fib 1)) (fib 2)) (fib 3))
(+ (+ (+ (+ 1 (fib 0)) (fib 1)) (fib 2)) (fib 3))
(+ (+ (+ (+ 1 0) (fib 1)) (fib 2)) (fib 3))
(+ (+ (+ 1 (fib 1)) (fib 2)) (fib 3))
(+ (+ (+ 1 1) (fib 2)) (fib 3))
(+ (+ 2 (fib 2)) (fib 3))
...

We see that the number of maximum number of deferred calls is proportional to the maximum depth of the tree. Thanks to prigoginic leap for the explanation.

The Fibonacci sequence can also be formulated as an iterative process. The idea is to use a pair of numbers, initialised to $\mathrm{Fib}(1)=1$ and $\mathrm{Fib}(0)=0$, and to repeatly apply the simultaneous transformations

$\begin{align} a &\leftarrow a + b\\\\ b &\leftarrow a \end{align}$

Thus we can compute Fibonacci numbers using the preocedure

(define (fib n)
  (fib-iter 1 0 n))
  
(define (fib-iter a b count)
  (if (= count 0)
      b
      (fib-iter (+ a b) a (- count 1))))

This scond mehtod for computing $\mathrm{Fib}(n)$ is a linear iteration.

Orders of Growth

The notion of orders of growth provides a gross measure of the resources required by a process as the inputs becomes larger.

Let $n$ be a parameter that measures the size of the problem, and let $R(n)$ be the amount of resources the process requires for a problem of size $n$. We say that $R(n)$ has order of growth $\Theta(f(n))$, written $R(n)=\Theta(f(n))$, if there are positive constants $k_1$ and $k_2$ independent of $n$ such that

$k_1f(n)\le R(n)\le k_2f(n)$

for any sufficiently large value of $n$.

Exponentiation

We would like to write a procedure that takes as arguments a base $b$ and a positive integer exponent $n$ and computes $b^n$. One way to do this is via the recursive definition

$\begin{align} b^n &= b\cdot b^{n-1}\\\\ b^0 &= 1 \end{align}$

which can be translated into the procedure

(define (expt b n)
    (if (= n 0)
        1
        (* b (expt b (- n 1)))))

This is a linear recursive process, which requires $\Theta(n)$ steps and $\Theta(n)$ space. We can easily write an iterative version which will require $\Theta(n)$ steps and $\Theta(1)$ space.

The number of steps can be reduced by using successive squaring, that is,

$b^n=\begin{cases} (b^{n/2})^2\qquad&\text{if $n$ is even}\\\\ b\cdot b^{n-1} &\text{if $n$ is odd} \end{cases}$

(define (fast-expt b n)
    (cond ((= n 0) 1)
          ((even? n) (square (fast-expt b (/ n 2))))
          (else (* b (fast-expt b (- n 1))))))

where even? is a primitive procedure.

Space and steps grow at logrithmically with $n$ in this process.

:testSite

work in progress

1.2 Procedures and the Processes They Generate

Linear Recursion and Iteration

Tree Recursion

Orders of Growth

Exponentiation