Exercise 2.63 -- 2.65
Exercise 2.63
Each of the following procedures converts a binary tree to a list.
(define (tree->list-1 tree)
(if (null? tree)
'()
(append (tree->list-1 (left-branch tree))
(cons (entry tree)
(tree->list-1 (right-branch tree))))))
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if (null? tree)
result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list
(right-branch tree)
result-list)))))
(copy-to-list tree '()))- Do the two procedures produce the same results for every tree? If not, how do the results differ? What lists do the two procedures produce fot the trees in Figure 2.16?
- Do the two proceudres have the same order of growth in the number of steps required to convert a balanced tree with $n$ elements to a list? If not, which one grows more slowly?
Solution
The two tree-to-list procedures produce the same results for all trees. For example:
(define tree1 '(7 (3 (1 () ()) (5 () ())) (9 () (11 () ()))))
(define tree2 '(3 (1 () ()) (7 (5 () ()) (9 () (11 () ())))))
(define tree3 '(5 (3 (1 () ()) ()) (9 (7 () ()) (11 () ()))))
(tree->list-1 tree1)
; (1 3 5 7 9 11)
(tree->list-2 tree1)
; (1 3 5 7 9 11)
(tree->list-1 tree2)
; (1 3 5 7 9 11)
(tree->list-2 tree2)
; (1 3 5 7 9 11)
(tree->list-1 tree3)
; (1 3 5 7 9 11)
(tree->list-2 tree3)
; (1 3 5 7 9 11)The difference between the two procedures is that whereas
tree->list-1 uses append to collate sub-lists tree->list-2,
through the helper function copy-to-list, stores the state in the
result-list variable.
Through the use of the helper function, tree->list-2 avoids the
second recursion that happens when calling append and so takes less
steps. That is, the first is an recursive process and the second an
interative process.
Exercise 2.64
The following procedure list->tree converts an ordered list to a
balanced binary tree. The helper procedure partial-tree takes as
arguments an integer $n$ and list of at least $n$ elements and
constructs a balanced tree containing the first $n$ elements of the
list. The result returned by partial-tree is a pair (formed with
cons) whose car is the constructed tree and whose cdr is the
list of elements not included in the tree.
(define (list->tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0)
(cons '() elts)
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result (partial-tree elts left-size)))
(let ((left-tree (car left-result))
(non-left-elts (cdr left-result))
(right-size (- n (+ left-size 1))))
(let ((this-entry (car non-left-elts))
(right-result (partial-tree
(cdr non-left-elts)
right-size)))
(let ((right-tree (car right-result))
(remaining-elts (cdr right-result)))
(cons (make-tree
this-entry left-tree right-tree)
remaining-elts))))))))- Write a short paragraph explaining as clearly as you can how
partial-treeworks. Draw the tree produced bylist->treefor the list(1 3 5 7 9 11). - What is the order of growth in the number of steps required by
list->treeto convert a list of $n$ elements?
Solution
The partial-tree procedure is a recursive process which splits the
ordered elements list into halves from which it bulids the left and
right branches of the tree.
(list->tree (list 1 3 5 7 9 11))
; (5 (1 () (3 () ())) (9 (7 () ()) (11 () ())))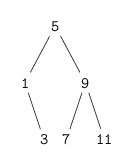
Tikz code here
As the partial-tree procedure makes a tree for every element of the
list the growth in the number of steps for the procedure, and hence
for list->tree, is $\Theta(n)$.
Exercise 2.65
Use the results of Exercise 2.63 and
Exercise 2.64 to give $\Theta(n)$ implementations of
union-set and intersection-set for sets implemented as (balanced)
binary trees.
Solution
In Exercise 2.63 and Exercise 2.64 we have
procedures to convert trees to lists and list to trees in $\Theta(n)$
steps. Previously we have developed procedures for the
union and
intersection
of ordered sets also in $\Theta(n)$ steps. So to implement union-set
and intersection-set for binary trees:
- Convert the trees to ordered lists using
tree->list - Get the union/intersection as an ordered list using
union-setandintersection-setfor ordered lists - Convert the resulting ordered list to binary tree using
list->tree
(define (union-set set1 set2)
(list->tree (union-set-list (tree->list set1)
(tree->list set2))))
(define (intersection-set set1 set2)
(list->tree (intersection-set-list (tree->list set1)
(tree->list set2))))As the conversions and set operations are $\Theta(n)$, their serial composite is also $\Theta(n)$.