Exercise 2.24 -- 2.29
Exercise 2.24
Suppose we evaluate the expression
(list 1 (list 2 (list 3 4)))Give the result printed by the interpreter, the corresponding box-and-pointer structure, and the interpretation of this as a tress.
Solution
(list 1 (list 2 (list 3 4)))
; (1 (2 (3 4)))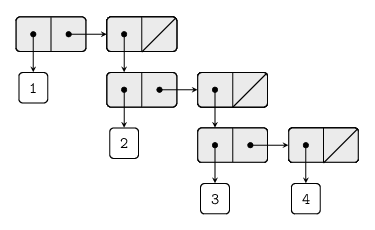
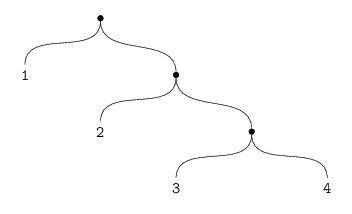
Exercise 2.25
Give combinations of cars and cdrs that will pick 7 from each of
the following lists:
(1 3 (5 7) 9)
((7))
(1 (2 (3 (4 (5 (6 7))))))Solution
(define x (list 1 3 (list 5 7) 9))
(car (cdr (car (cdr (cdr x)))))
(define x (list (list 7)))
(car (car x))
(define x (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7)))))))
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr x))))))))))))Exercise 2.26
Suppose we define x and y to be two lists:
(define x (list 1 2 3))
(define y (list 4 5 6))What results is printed by the interpreter in response to evaluating each of the following expressions:
(append x y)
(cons x y)
(list x y)Solution
(append x y)
; (1 2 3 4 5 6)
(cons x y)
; ((1 2 3) 4 5 6)
(list x y)
; ((1 2 3) (4 5 6))Exercise 2.27
Modify your reverse procedure of
Exercise 2.18
to produce a deep-reverse procedure that takes a list as argument
and returns as its value a list with its elements reverse and with all
sublists deep-reversed as well. For example,
(define x (list (list 1 2) (list 3 4)))
x
; ((1 2) (3 4))
(reverse x)
; ((3 4) (1 2))
(deep-reverse x)
((4 3) (2 1))Solution
(define (deep-reverse items)
(define (reverse-iter items rev-items)
(cond ((null? items) rev-items)
((not (pair? items)) items)
(else (reverse-iter (cdr items)
(cons (deep-reverse (car items))
rev-items)))))
(reverse-iter items '()))Exercise 2.28
Write a procedure fringe that takes as argument a tree (represented
as a list) and returns a list whose elements are all the leaves of the
tree arranged in left-to-right order. For example
(define x (list (list 1 2) (list 3 4)))
(fringe x)
; (1 2 3 4)
(fringe (list x x))
; (1 2 3 4 1 2 3 4)Solution
(define (fringe items)
(cond ((null? items) items)
((not (pair? items)) (list items))
(else (append (fringe (car items))
(fringe (cdr items))))))Exercise 2.29
A binary mobile consists of two branches, a left branch and a right
branch. Each branch is a rod of a certain length, from which hangs
either a weight or another binary mobile. We can represent a binary
mobile using compound data by constructing it from two branches (for
example, using list):
(define (make-mobile left right)
(list left right))A branch is constructed from a length (which must be a number)
together with a structure, which may be wither a number
(representing a simple weight) or another mobile:
(define (make-branch length structure)
(list length structure))- Write the corresponding selectors
left-branchandright-branchwhich return the branches of a mobile, andbranch-lengthandbranch-structure, which return the compoments of a branch. - Using your selectors, define a procedure
total-weightthat returns the total weight of a mobile. - A mobile is said to be balanced if the torque applied by its top left branch is equal to that applied by its top right branch (that is, if the length of the left rod multiplied by the weight from that rod is equal to the corresponding product for the right side) and if each of the submobiles hanging off its branches is balanced. Design a predicate that tests whether a binary mobile is balanced.
- Suppose that we change the representation of mobiles so that the constructors are
(define (make-mobile left right)
(cons left right))
(define (make-branch length structure)
(cons length structure))How much do you need to change your program to convert to the new represenation?
Solution
The selectors for mobiles and branches:
(define (left-branch mobile)
(car mobile))
(define (right-branch mobile)
(cadr mobile))
(define (branch-length branch)
(car branch))
(define (branch-structure branch)
(cadr branch))To define the total-weight procedure we also define helper procedure,
branch-weight
(define (branch-weight branch)
(if (pair? (branch-structure branch))
(total-weight (branch-structure branch))
(branch-structure branch)))
(define (total-weight mobile)
(+ (branch-weight (left-branch mobile))
(branch-weight (right-branch mobile))))We first define a procedure that calculates the torque of a branch,
then the balanced? predicate
(define (torque branch)
(* (branch-length branch)
(branch-weight branch)))
(define (balanced? mobile)
(and (= (torque (left-branch mobile))
(torque (right-branch mobile)))
(if (pair? (branch-structure (left-branch mobile)))
(balanced? (branch-structure (left-branch mobile)))
true)
(if (pair? (branch-structure (right-branch mobile)))
(balanced? (branch-structure (right-branch mobile)))
true)))If the representation of mobiles changes from using lists to cons only a couple of the selectors need to be changed
(define (right-branch mobile)
(cdr mobile))
(define (branch-structure branch)
(cdr branch))