2.3 Symbolic Data
All the compound data objects we have used so far were constructed ultimately from numbers. In this section we extend the representational capability of our lanaguage by introducing the ability to work with arbitrary symbols as data.
2.3.1 Quotation
If we can form compound data using symbols, we can have lists such as
(a b c d)
(23 45 17)
(((Norah 12) (Molly 9) (Anna 7) (Lauren 6) (Charlotte 4))
Lists containing symbols can look just like the expressions of our language:
(* (+ 23 45) (+ x 9))
(define (fact n) (if (= n 1) 1 (* n (fact (- n 1)))))In order to manipulate symbols we need a new element in our language:
the ability to quote a data object. Suppose we want to construct the
list (a b). We can’t accomplish this with (list a b), because this
expression constructs a list of the values of a and b rather
than the symbols themselves. This issue is well known in the context
of natural languages, where words and sentences may be regarded either
as sematic entities or as character strings (syntactic entities). The
common practice in natural languages is to use quotation marks to
indicate that a word or a sentence is to be treated literally as a
string of characters. For instance, the first letter of “John” is
clearly “J”. If we tell sombody “say your name aloud”, we expect to
hear that person’s name. However, if we tell somebody “say ‘your name’
alound”, we expect to hear words “your name”.
[Allowing quotation in a language wreaks havoc with the ability to reason about the language in simple terms, because ti destroys the notion that equals can be substituted for equals. For example, three is one plus two, but the word “three” is not the phrase “one plus two”. Quotation is powerful because it gives us a way to build expressions that manipulate other expressions. But allowing statements in a language that talk about other statements in that language makes it very difficult to maintatin any coherent princple of what “equals can be substituted for equals” should mean. For example, if we know that the evening star is the morning star, the from the statement “the evening star is Venus” we can deduce “the morning star is Venus”. However, given that “John knows that the evening star is Venus” we cannot infer that “John knows that the morning star is Venus”.]
We can follow this same practice to identify list and symbols that are
to be treated as data objects rather than as expressions to be
evaluated. However, our format for quoting differs from that of
natural languages in that we place a quotation mark (traditionally,
that single quote symbol, ') only at the beginning of the object to
be quoted. We can get away with this in Scheme syntax because we rely
on blanks and parentheses to delimit objects. Thus, the meaning of the
single quote character is to quote the next object.
Now we can distinguish between symbols and their values:
(define a 1)
(define b 2)
(list a b)
; (1 2)
(list 'a 'b)
; (a b)
(list 'a b)
; (a 2)Quotation also allows us to type in compound objects, using the conventional printed representation for lists:
(car '(a b c))
; a
(cdr '(a b c))
; (b c)In keeping with this, we can obtain the empty list by evaluating '().
One additional primitive used in manipulating symbols is eq?, which
takes two symbols as arguments and tests whether they are the same.
Using eq?, we can implement a useful procedure called memq. This
takes two arguments, a symbol and a list. If the symbol is not
contained in the list (i.e., is not eq? to any item in the list),
then memq returns false. Otherwise, it returns the sublist of the
list beginning with the first occurrence of the symbol:
(define (memq item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq item (cdr x)))))For example, the value of
(memq 'apple '(pear banana prune))is false, whereas the value of
(memq 'apple `(x (apple sauce) y apple pear))is (apple pear).
2.3.2 Example: Symbolic Differentiation
As an illustration of symbol manipulation and a further illustration of data abstraction, consider the design of a procedure that performs symbolic differentiation of algebraic expressions. We would like the procedure to take as arguments an algebraic expression and a variable and to return the derivative of the expression with respect to the variable.
In developing the symbolic-differentiation program, we will follow the same strategy of data abdtraction that we followed in developing the rational number system. That is, we will first define a differentiation algorithm that operates on abstract objects such as “sums”, “products”, and “variables” without worrying about how these are to ve represented. Only afterward will we address the representation problem.
The differentiation program with abstract data
In order to keep things simple, we will consider a very simple symbolic-differentiation program that handles expressions that are built up using only the operations of addition and multiplication with two arguments. Differentiation of any such expression can be carried out by applying the following reduction rules:
for $c$ a constant or a variable different from $x$,
Observe that the latter two are recursive in nature. That is, to obtain the serivative of a sum we first find the derivative of the terms and add them. Each of the terms may in turn be an expression that needs to be decomposed. Decomposition into smaller pieces will eventually produce pieces that are either contants or variables, whose derivatives wull be either 0 or 1.
To embody these rules in a procedure we indulge in a little wishful thinking, as we did in designing the rational number implementation. If we had a means for representing algerbraic expressions, we should be able to tell whether an expression is a sum, a product, a constant, or a variable. We should be able to extract the parts of an expression. For a sum, for example we want to be able to extract the addend (first term) and the augend (second term). We should also be able to construct expressions from parts. Let us assume that we already have procedures to implement the following selectors, constructors and predicates:
(variable? e) ; is e a variable?
(same-variable? v1 v2) ; are v1 and v2 the same variable?
(sum? e) ; is e a sum?
(addend e) ; addend of the sum e
(augend e) ; augend of the sum e
(make-sum a1 a2) ; construct the sum of a1 and a2
(product? e) ; is e a product?
(multiplier e) ; multiplier of the product e
(multiplicand e) ; multiplicand of the product e
(make-product m1 m2) ; construct the product of m1 and m2Using these, and the primitive predicate number?, which identifies
numbers, we can express the differentiation rules as the following
procedure:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type - DERIV" exp))))This deriv procedure incorporates the complete differentiation
algorithm. Since it is expressed in terms of abstract data, it will
work no matter how we choose to represent algebraic expressioins, as
long as we design a proper set of selectors and constructors, This is
the issue we must address next.
Representing algebraic expressions
We can imagine many ways to use list structure to represent algebraic
expressions. For example, we could use lists of symbols that mirror
the usual algebraic notation, representing $ax + b$ as the list
(a * x + b). However, one especially straightforward choise is to
use that same parenthesized prefix notation that Lisp uses for
combinations; that is, to represent $ax + b$ as (+ (* a x) b). Then
our data representation for the differentiation problem is as follows:
-
The variables are symbols. They are identified by the primitive predicate
symbol?(define (variable? x) (symbol? x)) -
Two variables are the same if the symbols representing them are
eq?:(define (same-variable? v1 v2) (and (variable? v1) (variable? v2) (eq? v1 v2))) -
Sums and products are constructed as lists:
(define (make-sum a1 a2) (list '+ a1 a2)) (define (make-product m1 m2) (list '* m1 m2)) -
A sum is a list whose first element is the symbol
+:(define (sum? x) (and (pair? x) (eq? (car x) '+))) -
The addend is the second item of the sum list:
(define (addend s) (cadr s)) -
The augend is the third item if the sum list:
(define (augend s) (caddr s)) -
A product is a list whose first element is the symbol
*:(define (product? x) (and (pair? x) (eq? (car x) '*))) -
The multipler is the second list of the product list:
(define (multiplier p) (cadr p)) -
The multiplicand is the third item of the product list:
(define (multiplicand p) (caddr p))
Thus, we need only combine these with the algorithm as embodied by
deriv in order to have a working symbolic-differentiation program.
Let us look at some examples of its behaviour:
(deriv '(+ x 3) 'x)
;(+ 1 0)
(deriv '(* x y) 'x)
;(+ (* x 0) (* 1 y))
(deriv '(* (* x y) (+ x 3)) 'x)
;(+ (* (* x y) (+ 1 0))
; (* (+ (* x 0) (* 1 y))
; (+ x 3)))The program produces answers that are correct; however, they are
umsimplified. We would like the program to know that $x\cdot 0=1$,
$1\cdot y=y$, and $0 + y=y$. The answer for the second example should
have been simply y. As the thrid example shows, this becomes a
serious issue when the expressions are complex.
Our difficulty is much like the onw we encountered with the rational
number implementation: we haven’t reduced answers to simplist form. To
accomplish the rational number reduction, we needed to change only the
constructors and the selectors of the implementation. We can adopt a
similiar strategy here. We won’t change deriv at all. Instead, we
will change make-sum so that if both summands are numbers, make-sum
will add them and return their sum. Also, if one of the summands is 0,
then make-sum will return the other summand.
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list '+ a1 a2))))This uses the procedure =number?, which checks whether an expression
is equal to a given number:
(define (=number? exp num)
(and (number? exp) (= exp num)))Similary, we will change make-product:
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2))))Here is how this version works on our three examples:
(deriv '(+ x 3) 'x)
; 1
(deriv '(* x y) 'x)
; y
(deriv '(* (* x y) (+ x 3)) 'x)
; (+ (* x y) (* y (+ x 3)))Although this is quite an improvement, the third example shows that there is still a long way to go before we get a program that puts expressions into a form that we might agree is “simplest”. The problem of algebraic simplification is complex because, among other reasons, a form that may be simplest for one purpose may not be for another.
2.3.3 Example: Representing Sets
In the previous examples we built representations for two kinds of compound data objects: rational numbers and algebraic expressions. In one of these examples we had the choice of simplifying (reducing) the expressions at either construction time or slection time, but other than that the choice of a representation for these structures in terms of lists was straightforward. When we turn to the representation of sets, the choice of a representation is not so obvious. Indeed, there are a number of possible representations, and they differ significantly from one another in several ways.
Informally, a set is simply a collection of distinct objects. To give
a more precise definition we can employ the method of data abstraction.
That is, we define “set” by specifying the operations that are to be
used on sets. These are union-set, intersection-set,
element-of-set?, and adjoin-set. Element-of-set? is a predicate
that determines whether a given element is a member of the set.
Adjoin-set takes an object and a set as arguments and returns a set
that contains the elements of the original set and also the adjoined
element. Union-set computes the union of two sets, which is the set
containing each element that appears in either argument.
Interaction-set computes that intersection of two sets, which is the
set containing only elements that appear in both arguments. From the
viewpoint of data abstractioni, we are free to design any
representation that implements these operations in a way consistent
with the interpretations given above.
If we want to be more formal, we can specify “consistent with the interpreations given above” to mean that the operations satisfy a collection of rules such as these:
- For any set
Sand any objectx,(element-of-set? x (adjoin-set x S)is true. - For any set
SandTand any objectx,(element-of-set? x (union S T))is equal to(or (element-of-set? x S) (element-of-set? x T)). - For any object
x,(element-of-set? x '())is false.
Sets as unordered lists
One way to represent a set is as a list of its elements in which no
element appreas more than once. The empty set is represented by the
empty list. In this representation, element-of-set? is similar to
the procedure memq. It uses equal? instead of eq? so that the
set elements need not be symbols:
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))Using this, we can write adjoin-set. If the object to be adjoined is
already in the set, we just return the set. Otherwise, we use cons
to add that object to the list that represents the set:
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))For intersection-set we can use a recursive strategy. If we know how
to form the intersection of set2 and the cdr of set1, we only
need to decide whether to include the car of set1 in this. But
this depends on whether (car set) is also in set2. Here is the
resulting procedure:
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))In desigining a representation, one of the issues we should be
concerned with is consistency. Consider the number of steps required
by our set operations. Since they all use element-of-set?, the
speed if this operation has a major impact on the efficiency of the
set implmentation as a whole. Now, in order to check whether an object
is a member of a set, element-of-set? may have to scan the entire
set. (In the worst case, the object turns out not to be in the set.)
Hence, if the set has $n$ elements, element-of-set? might take up to
$n$ steps. Thus, the number od steps required grows as $\Theta(n)$.
The number of steps required by adjoined-set, which use this
operation, also grows as $\Theta(n)$. For intersection-set, which
does an element-of-set? check for each element if set1, the number
of steps required grows as the product of the sizes of the sets
invovled, or $\Theta(n^2)$ for two sets of size $n$. The same will be
true of union-set.
Set as ordered lists
One way to speed up set operations is to change the representation so
that the set elements are listed in increasing order. To do this, we
need some way to compare two objects so that we can say which is
bigger. For example, we could compare symbols lexicographically, or we
could agree on some method for assigning a unique number to an object
and then compare the elements by comparing the corresponding numbers.
To keep our discussion simple, we will consider only the case where
the set elements are numbers, so that we can compare elements using
< and >. We will represent a set of numbers by listing its
elements in increasing order. Whereas our first representation above
allowed us to represent the set {1, 3, 6, 10} in any order, our new
representation allows only the list (1 3 6 10).
One advantage of ordering shows up in element-of-set?: in checking
for the presence of an item, we no longer have to scan the entire set.
If we reach a set element that is larger that the item we are looking
for, then we know that the item is not in the set:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (car set)) true)
((< x (car set)) false)
(else (element-of-set? x (cdr set)))))How many steps does this save? In the worse case, the item we are looking for may be the largest one in the set, so the number of steps is the same for the unordered representation. On the other hand, if we search for items of many different sizes we can expect that sometimes we will be able to stop searching at a point near the begining of the list. On average we should expect to have to examine about half of the items in the set. Thus, the average number of steps required will be about $n/2$. This is still $\Theta(n)$ growth, but it does save us, on average, a factor of 2 in number of steps over the previous implementation.
We obtain a more impressive speedup with intersection-set. In the
unordered representation this operation required $\Theta(n^2)$ steps,
because we performed a complete scan of set2 for each element of
set1. But with ordered representation, we can use a more clever
method. Begin by comparing initial elements, x1 and x2, of the two
sets. If x1 equals x2, then that gives an element of the
intersection, and the rest of the intersection is the intersection of
the cdr-s of the two sets. Suppose, however, that x1 is less than
x2. Since x2 is the smallest element in set2, we can immediately
conclude that x1 cannot appear anywhere in set2 and hence is not
in the intersection. Hence, the intersection is equal to the
intersection of set2 with the cdr of set1. Similarly, if x2 is
less that x1, then the intersection is given by the intersection of
set1 with the cdr of set2. Here is the procedure:
(define (intersection-set set1 set2)
(if (or (null? set1) (null? set2))
'()
(let ((x1 (car set1)) (x2 (car set2)))
(cond ((= x1 x2)
(cons x1 (intersection-set (cdr set1)
(cdr set2))))
((< x1 x2)
(intersection-set (cdr set1) set2))
((< x2 x1)
(intersection-set (set1 (cdr set2))))))))To estimate the number of steps required by this process, observe that
at each step we reduce the intersection problem to computing
intersection of smaller sets – removing the first element from set1
or set2 or both. Thus, the number of steps required is at most the
sum if the sizes of set1 and set2, rather than the product of the
sizes as with the unordered representation. This is $\Theta(n)$ growth
rather than $\Theta(n^2)$ – a considerable speedup, even for sets of
moderate size.
Sets as binary trees
We can do better than the ordered-list representation by arranging the set elements in the form of a tree. Each node of the tree holds one element of the set, called the “entry” at that node, and a link to each of two other (possibly empty) nodes. The “left” link points to elements smaller than the one at the node, and the “right” link to elements greater than the one at the node. The figure below shows some trees that represent the set ${1,3,5,7,9}$. The same set may be represented by a tree in a number of different ways. The only thing we require for a valid representation is that all elements in the left subtree be smaller than the node entry and that all elements in the right subtree be larger.
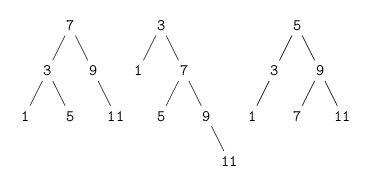
Tikz code here
The advantage of the tree representation is this: suppose we want to check whether a number $x$ is contained in a set. We begin by conparing $x$ with the entry in the top node. If $x$ is less than this, we know that we need only search the left subtree; it $x$ is greater, we need only search the right subtree. Now, if the tree is “balanced”, each if these subtrees will be about half the size of the original. Thus, in one step we have reduced the problem of searching a tree of size $n$ to searching a tree of size $n/2$. Since the size of the tree is halved at each step, we should expect that the number of steps needed to search a tree of size $n$ grows as $\Theta(\log n)$. For large sets, this will be a significant speedup over the previous representations.
We can represent trees by using lists. Each node will be a list of three items: the entry at the node, the left subtree, and the right subtree. A left or a right subtree of the empty list will indicate that there is no subtree connected there. We can describe this representation by the following procedures:
(define (entry tree) (car tree))
(define (left-branch tree) (cadr tree))
(define (right-branch tree) (caddr tree))
(define (make-tree entry left right)
(list entry left right))Now we can write the element-of-set? procedure using the strategy
decribed above:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (entry set)) true)
((< x (entry set))
(element-of-set? x (left-branch set)))
((> x (entry set))
(element-of-set? x (right-branch set)))))Ajoining an item to a set is implemented similarly and also requires
$\Theta(\log n)$ steps. To adjoin an item x, we compare x with the
node entry to determine whether x should be added to the right or to
the left branch, and having adjoined x to the appropriate branch we
piece this newly constructed branch together with the original entry
and the oter branch. If x is equal to the entry, we just return the
node. If we are asked to adjoin x to an empty tree, we generate a
tree that has x as the entry and empty right and left branches. Here
is the procedure:
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree (entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree (entry set)
(left-branch set)
(adjoin-set x (right-branch set))))))The above claim that searching the tree can be performed in a
logarithmic number of steps rests on the assumption that the tree is
“balanced,” i.e., that the left and right subtrees of every tree have
approximately the same number of elements, so that each subtree
contains about half the elements of its parent. But how can we be
certain that the trees we construct will be balanced? Even if we start
with a balanced tree, adding elements with adjoin-set may produce an
unbalanced result. Since the position of a newly adjoined element
depends on how the element compares with the items already in the set,
we can expect that if we add elements “randomly” the tree will tend to
be balanced on the average. But this is not a guarantee. For example,
if we start with an empty set and adjoin the numbers from 1 through 7
in sequence we end up a highly unbalanced tree. In this tree all the
left subtrees are empty, so it has no advantage over an ordered list.
One way to solve this problem is to define an operation that
transforms an arbitrary tree into a balanced tree with the same
elements. Then we can perform this transformation after every few
adjoin-set operations to keep out set in balance. There is also
other ways to solve this problem, most of which involve designing new
data structures for which searching and insertion both can be done in
$\Theta(\log n)$ steps.
Sets and information retrieval
We have examined options for using lists to represent sets and have seen how the choice of representation for a data object can have a large impact on the performance of the programs that use the data. Another reason for concentrating on sets is that the techniques discussed hare appear again and again in applications involving information retrivial.
Consider a data base containing a large number of individual records, such as the personnel files for a company or the transactions in an accounting system. A typical data-management system spends a large amount of time accessing or modifying the data in the records and therefore requires an efficient method for accessing records. This is done by identifying a part of each record to serve as an identifying key. A key can be anything that uniquely identifies the record. For a personnel file, it might be an employee’s ID number. For an accounting system, it might be a transaction number. Whatever the key is, when we define the record as a data structure we should includ a key selector procedure that retrieves the key associated with a given record.
Now we represent the data base as a set of records. To locate the
record with a given key we use a procedure lookup, which takes as
arguments a key and a data base and which returns the record that has
that key, or false if there is no such record. Lookup is implemented
in almost the same way as element-of-set?. For example, if the set
of records is implemented as an unordered list, we could use
(define (lookup given-key set-of-records)
(cond ((null? set-of-records) false)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
(else (lookup given-key (cdr set-of-records)))))Of course, there are better ways to represent large sets than as unordered lists. Information-retrieval systems in which records have to be “randomly accessed” are typically implemented by a tree-based method, such as the binary-tree representation discussed previously. In designing such a system the methodology of data abstraction can be a great help. The designer can create an initial implementation using a simple, straightforward representation such as unordered lists. This will be unsuitable for the eventual system, but it can be useful in providing a “quick and dirty” data base with whci to test the rest of the system. Later on, the data representation can be modified to be more sophisticated. If the data base is accessed in terms of abstract selectors and constructors, this change in representation will not require any changes to the rest of the system.
2.3.4 Example: Huffman Encoding
This section provides practice in the use of list structures and data abstraction to manipulate sets and trees. The application is to methods for representing data as sequences of ones and zeros (bits). For example, the ASCII standard code used to represent text in computers encodes each character as a sequence of seven bits. Using seven bits allows us to distinguish $2^7$ or 128, possible different characters. In general, if we want to distinguish $n$ different symbols, we will need to use $\log_2n$ bits per symbol. If all our messages are made up of the eight symbols A, B, C, D, E, F, G, H, we can choose a code with three bits per character, for example
A 000 C 010 E 100 G 110
B 001 D 011 F 101 H 111
With this code, the message
BACADAEAFABBAAAGAH
is encoded as the string of 54 bits
001000010000011000100000101000001001000000000110000111
Code such as ASCII and the A-through-H above are knows as fixed-length codes, because they are represent each symbol in the message with the same number of bits. It is sometimes advantageous to use variable-length codes, in which different symbols may be represented by different number of bits. For example, Morse code does not use the same number of dots and dashs for each letter of the alphabet. In particular, E, the most frequent letter, is represented by a single dot. In general, if our messages are such that some symbols appear very frequently and some very rarely, we can encode data more efficiently (i.e., using fewer bits per message) if we assign shorter codes to the frequent symbols. Consider the following alternative code for the letters A through H:
A 0 C 1010 E 1100 G 1110
B 100 D 1011 F 1101 H 1111
With this code, the same message as above is encoded as the string
100010100101101100011010100100000111001111
This string contains 42 bits, so it saves more than 20% in space in comparison with the fixed-length code shown above.
One of the difficulties of using variable-length code is knowing when you have reached the end of a symbol in readin a sequence of zeros and ones. Morse code solves this problem by using a special separator code (in this case a pause) after the sequence of dots and dashes for each letter. Anoterh solution is to design the code in such a way that no complete code for any symbol is the beginning (or prefix) of the code for another symbol. Such a code is called a prefix code. In the example above, A is encoded by 0 and B is encoded 100, so no other symbol can have a code that begins with 0 or with 100.
In general, we can attain significant savings if we use variable-length prefix codes that take advantage of the relative frequencies of the symbols on the messages to be encoded. One particular scheme for doing this is called the Huffman encoding method, after its discoverer, David Huffman. A Huffman code can be represented as a binary tree whose leaves are the symbols that are encoded. At each non-leaf node of the tree there is a set containing all the symbols in the leaves that lie below the node. In addition, each symbol at a leaf is assigned a weight (which is its relative frequency), and each non-leaf node contains a weight that is the sum of all the weights of the leaves below it. The weights are not used in the encoding or the decoding process. We will see below how they are used to help construct the tree.
The figure below shows the Huffman tree for the A-through-H code given above. The weight at the leaves indicate that the tree was designed for messages in which A appears with relative frequency 8, B with a relative frequency 3, and the other letters each with relative frequency 1.
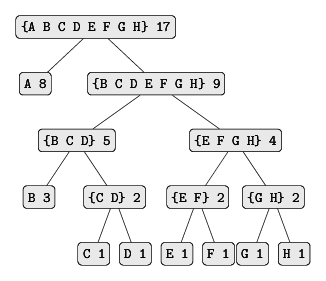
Tikz code here
Given a Huffman tree, we can find the encoding of any symbol by starting at the root and moving down until we reach the leaf that holds the symbol. Each time we move down a left branch we add a 0 to the code, and each time we move down a right branch we add a 1. (We decide which branch to follow by testing to see which branch either is the leaf node for the symbol or contains the symbol in its set.) For example, starting from the root of the tree, we arrive at the leaf for D by following a right branch, then a left branch, than a right branch: hence, the code for D is 1011.
To decode a bit sequence using a Huffman tree, we begin at the root and use the successive zeros and ones of the bit sequence to determine whether to move down the left or the right branch. Each time we come to a leaf, we have generated a new symbol in the message, at which point we start over from the root of the tree to find the next symbol.
Generating Huffman trees
Given an “alphabet” of symbols and their relative frequencies, how do we construct the “best” code? (In other words, which tree will encode messages with the fewest bits?) Huffman gave an algorithm for doing this and showed that the resulting code is indeed the best variable-length code for messages where the relative frequency of the symbols matches the frequencies with whch the code was constructed. We will not prove this optimality of Huffman codes here, but we will show how Huffman trees are constructed. [See Hamming 1980 for a discussion of the mathematical properties of Huffman codes.]
The algorithm for generating Huffman trees is very simple. The idea is to arrange the tree so that the symbols with the lowest frequency appear farthest away from the root. Begin with the set of leaf nodes, containing symbols and their frequencies, as determined by the initial data from which the code is to be constructed. Now find two leaves with the lowest weights and merge them to produce a node that has these two nodes as its left and right branches. The weight of the new node is the sum of the two weights. Remove the two leaves from the original set and replace them by this new node. Now continue this process. At each step, merge two nodes with the smallest weights, removing them from the set and replace them with a node that has these two as its left and right branches. The process stops when there is only one node left, which is the root of the entire tree. Here is how the Huffman tree of the figure above was generated:
Initial leaves {(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)}
Merge {(A 8) (B 3) ({C D} 2) (E 1) (F 1) (G 1) (H 1)}
Merge {(A 8) (B 3) ({C D} 2) ({E F} 2) (G 1) (H 1)}
Merge {(A 8) (B 3) ({C D} 2) ({E F} 2) ({G H} 2)}
Merge {(A 8) (B 3) ({C D} 2) ({E F G H} 4)}
Merge {(A 8) ({B C D} 5) ({E F G H} 4)}
Merge {(A 8) ({B C D E F G H} 9)}
Final merge {({A B C D E F G H} 17)}
The algorithm dose not always specify a unique tree, because there may not be unique smallest-weught nodes at each step. Also, the choice of the order on which the two nodes are merged (i.e., which will be the right branch and which will be the left branch) is arbitrary.
Representing Huffman trees
In the exercises below we will work with a system that uses Huffman trees to encode and decode messages and generates Huffman trees according to the algorithm outlined above. We will begin by dicussing how trees are represented.
Leaves of the tree are represented by a list consisting of the symbol
leaf, the symbol at the leaf, and the weight:
(define (make-leaf symbol weight)
(list 'leaf symbol weight))
(define (leaf? object)
(eq? (car object) 'leaf))
(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))A general tree will be a list of a left branch, a right branch, a set of symbols, and a weight. The set of symbols will be simply a list of the symbols, rather than some more sophisticated set representation. When we make a tree by merging two nodes, we obtain the weight of the tree as the sum of the weights of the nodes, and the set of symbols as the union of the sets of symbols for the nodes. Since our symbol sets are represented as lists, we can form the union by using the append procedure:
(define (make-code-tree left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))If we make a tree in this way, we have the following selectors:
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
(if (leaf? tree)
(list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))The procedure symbols and weight must do something slightly
different depending on whether they are called with a leaf or a
general tree. These are simple examples of generic procedures
(procedures that can handle more that on kind of data), which we will
have much more to say about in Section 2.4 and Section 2.5.
The decoding procedure
The following procedure implements the decodeing algorithm. It takes as arguments a list of zeros and ones, together with a Huffman tree.
(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch (car bits) current-branch)))
(if (leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit - CHOOSE-BRANCH" bit))))The procedure decode-1 takes two arguments: the list of remaining
bits and the current position in the tree. It keeps moving “down” the
tree, choosing a left or a right branch according to whether the next
bit in the list is a zero or a one. (This is done with the procedure
choose-branch.) When it reaches a leaf, it returns the symbol at
that leaf as the next symbol in the message by consing it onto the
result of the decodeing of the rest of the message, starting at the
root of the tree. Note the error check in the final clause of
choose-branch, which complains if the procedure finds something
other than a zero or a one in the input data.
Set of weighted elements
In our representation of trees, each non-leaf node contains a set of symbols, which we have represented as a simple list. However, the tree-generating algorithm discussed above requires that we also work with sets of leaves and trees, successively merging the two smallest items. Since we will be required to repeatedly find the smallest item in a set, it is convenient to use an ordered representation for this kind of set.
We will represent a set of leaves and trees as a list of elements,
arranged in increasing order of weight. The following adjoin-set
procedure for constructing sets is similar to the ones described in
Exercise 2.61;
however, items are compared by their weights, and the element being
added to the set is never already in it.
(define (adjoin-set x set)
(cond ((null? set) (list x))
((< (weight x) (weight (car set))) (cons x set))
(else (cons (car set)
(adjoin-set x (cdr set))))))The following procedure takes a list of symbol-frequency pairs such as
((A 4) (B 2) (C 1) (D 1)) and constructs an initial ordered set of
leaves, ready to be merged according to the Huffman algorithm:
(define (make-leaf-set pairs)
(if (null? pairs)
'()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair) ;symbol
(cadr pair)) ;frequency
(make-leaf-set (cdr pairs))))))