Exercise 2.2 -- 2.3
Exercise 2.2
Consider the problem of representing line segments in a plane. Each
segement is represented as a pair of points: a starting point and an
ending point. Define a constructor make-segment and selector
start-segment and end-segment that define the representation of
segments in terms of points. Furthermore, a point can be represented
as a pair of numbers: the x coordinate and the y coordinate.
Accordingly, specify a constructor make-point and selectors
x-point and y-point that defines this representation. Finally,
using your selectors and constructors, define a procedure
midpoint-segment that take a line segment as argument and returns
its midpoint (the point whose coordinates are the average of the
coordinates of the endpoints). To try you procedures, you’ll need a
way to point points:
(define (print-point p)
(newline)
(display "(")
(display (x-point p))
(display ",")
(display (y-point p))
(display ")"))Solution
; segment constructor and selectors
(define (make-segment start end)
(cons start end))
(define (start-segment seg)
(car seg))
(define (end-segment seg)
(cdr seg))
; point constructor and selectors
(define (make-point x y)
(cons x y))
(define (x-point pt)
(car pt))
(define (y-point pt)
(cdr pt))
; midpoint of segment
(define (midpoint-segment seg)
(let ((start (start-segment seg))
(end (end-segment seg)))
(make-point (avg (x-point start) (x-point end))
(avg (y-point start) (y-point end)))))
(define (avg a b)
(/ (+ a b) 2))An example:
(define a (make-point 0 0))
(define b (make-point 0 2))
(define s (make-segment a b))
(print-point (midpoint-segment s))
; (0,1)Exercise 2.3
Implement a representation for rectangles in a plane. (Hint: You might want to make use of Exercise 2.2 .) In terms of your constructors and selectors, create procedures that compute the perimeter and the area of a given rectangle. Now implement a different representation for rectangles. Can you design your system with suitable abstraction barriers so that the same perimeter and area procedures will work using either representation?
Solution
The first represenation uses a corner, the length, the width and orientation to define the rectangle:
; Add two points (vector addition)
(define (add-pts p1 p2)
(make-point (+ (x-point p1) (x-point p2))
(+ (y-point p1) (y-point p2))))
; Change from polar to cartesian coordinates
(define (polar2cart r theta)
(make-point (* r (cos theta))
(* r (sin theta))))
; pi
(define pi (acos -1))
; Representation of rectangle 1:
; l: float, length
; w: float, width
; p: point, left-most, then lowest point of rectangle
; a: float, angle from horizontal to length edge of rectangle
; (in radians, on the interval (-0.5,0.5])
; Returns a list of l, w, a and the corners c1,...,c4
(define (make-rect l w p a)
(let ((c2 (if (> a 0)
(add-pts p (polar2cart l (* a pi)))
(add-pts p (polar2cart w (* (+ a 0.5) pi)))))
(c3 (if (> a 0)
(add-pts p (polar2cart (sqrt (+ (* l l) (* w w)))
(- (* a pi) (atan (/ w l)))))
(add-pts p (polar2cart (sqrt (+ (* l l) (* w w)))
(+ (* a pi) (atan (/ w l)))))))
(c4 (if (> a 0)
(add-pts p (polar2cart w (* (- a 0.5) pi)))
(add-pts p (polar2cart l (* a pi))))))
(cons l
(cons w
(cons a
(cons p
(cons c2
(cons c3 c4))))))))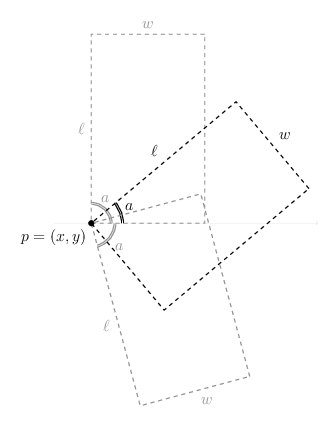 Tikz code for image on Github
Tikz code for image on Github
The second representation uses two points and an angle of orientation:
; rotate vector by 180 degrees
(define (neg-pt pt)
(cons (- (x-point pt)) (- (y-point pt))))
; difference of two vectors
(define (subt-pts p1 p2)
(add-pts p1 (neg-pt p2)))
; scalar multiplication of a vector
(define (scalar-mult a p)
(make-point (* a (x-point p)) (* a (y-point p))))
; dot/inner product of two vectors
(define (dot-prod p1 p2)
(+ (* (x-point p1) (x-point p2)) (* (y-point p1) (y-point p2))))
; Representation of rectangle 2:
; p1, p2: points, opposite corners of rectangle
; a: float, angle of an edge to horizontal (radians in
; interval -0.5,0.5)
; Returns a list of dim1, dim2, a and the corners c1,...,c4
(define (make-rect p1 p2 a)
(let ((d (subt-pts p2 p1))
(v1 (polar2cart 1 (* a pi)))
(v2 (polar2cart 1 (* (+ a 0.5) pi))))
(cons (abs (dot-prod d v1))
(cons (abs (dot-prod d v2))
(cons a
(cons p1
(cons (add-pts p1 (scalar-mult (dot-prod d v1)
v1))
(cons p2
(add-pts p1 (scalar-mult (dot-prod d v2)
v2))))))))))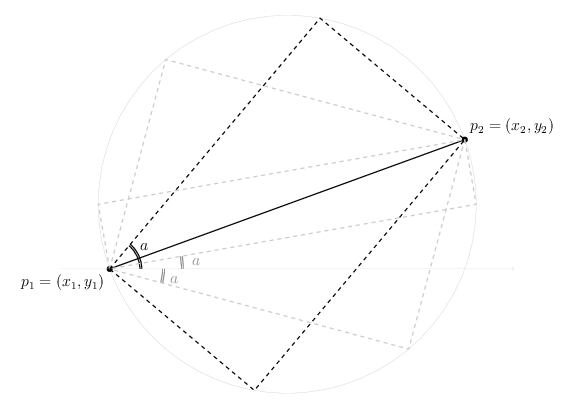 Tikz code for image on Github
Tikz code for image on Github
Since both representations of the rectange return the properties of the rectangle in the same form, we can use common selector procedures for both represenations, and hence, common area and perimeter procedures:
; Selectors
(define (rect-length rect)
(car rect))
(define (rect-width rect)
(car (cdr rect)))
; Procedures on rectangle
(define (rect-area rect)
(* (rect-length rect) (rect-width rect)))
(define (rect-perimeter rect)
(+ (* 2 (rect-length rect)) (* 2 (rect-width rect))))